Geosynchronous Orbits are WEIRD

????

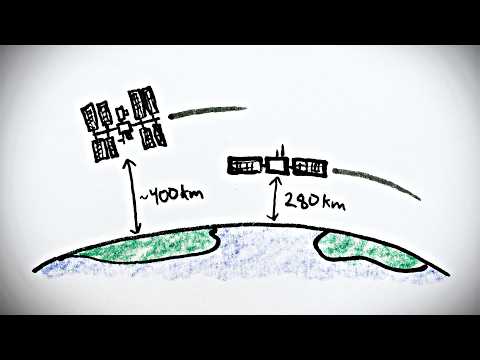
Go to https://givewell.org/minutephysics to have your first donation matched up to $100! This video is about the physics of geosynchronous and geostationary orbits, why they exist, when they don't, when they're useful for communication/satellite TV, etc. REFERENCES Fraction of a sphere that's visible from a given distance https://math.stackexchange.com/questions/1329130/what-fraction-of-a-sphere-can-an-external-observer-see Orbital period https://en.wikipedia.org/wiki/Orbital_period Kepler's third law https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion#Third_law Kepler's 3rd law (which can be derived from Newton's law of gravitation and the centripetal force necessary for orbit as mr\omega^2=G\frac{mM}{r^2}, and using \omega=\frac{2\pi}{T}) is T = 2pi Sqrt(r^3/(GM)) where M is the mass of the central object, G is the gravitational constant. Alternatively, we can solve for r, r = (T^2/(4pi^2) GM)^(1/3) ~ T^(2/3)/M^(1/3) = (T^2/M)^(1/3). There is a limit (kind of like the Roche limit but for rotations). A rotating solid steel ball or other chunk of metal that has tensile strength (ie that isn't just a pile of stuff held together by gravity like most planets) would be able to spin faster. Calculate how much of a planet's surface you can see from a given geosynchronous orbit/radius? (Obviously for lower ones you can see less, etc) - d/(2(R+d)) where d is distance to surface, ie, R is sphere radius, R+d is object radius from sphere center. Let's plug that in with r being the geostationary orbit radius. That is, we have \frac{1}{2} \left(1- \left(\frac{4 \pi^2 R^3}{T^2 G M }\right)^{1/3}\right) Average density of a sphere \rho is given by \rho =M/(\frac{4}{3}\pi R^3), ie \rho=\frac{3M}{4 \pi R^3} aka \frac{M}{R^3}=\frac{4}{3}\pi \rho. So we can convert the "fraction of planet surface seen" to \frac{1}{2} \left(1- \left(\frac{3 \pi}{G \rho T^2}\right)^{1/3}\right) So as either \rho or T\to \infty, the fraction goes to a maximum of \frac{1}{2}. And the point of "singularity" where the orbit coincides with the surface is where G\rho T^2=3\pi, aka \rho=\frac{3\pi}{GT^2}. For a rotation period of 3600s, that corresponds to a density \rho \approx 11000kg/m^3, which is roughly twice the density of the earth. For a rotation period of 5400s, we have \rho\approx 4800kg/m^3, which is basically the density of the earth. Alternately, if we plug the density of the earth in to an orbit of period 5400s, we get as a fraction of the planet seen: \frac{1}{2} \left(1- \left(\frac{3 \pi}{G \rho T^2}\right)^{1/3}\right) = 0.02 aka 2\% of the earth's surface. Support MinutePhysics on Patreon! http://www.patreon.com/minutephysics Link to Patreon Supporters: http://www.minutephysics.com/supporters/ MinutePhysics is on twitter - @minutephysics And facebook - http://facebook.com/minutephysics Minute Physics provides an energetic and entertaining view of old and new problems in physics -- all in a minute! Created by Henry Reich