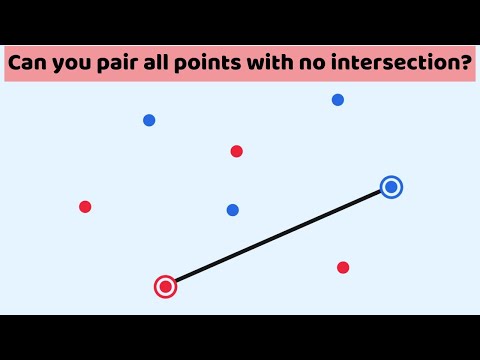
Can you (always) pair an equal number of red and blue points such that no line segments intersect?
Next video (on Odysee): https://odysee.com/@ZachStar:0/max-distance-puzzle:f My Odysee Channel: https://odysee.com/@ZachStar:0 STEMerch Store: https://stemerch.com/ ?Follow me Odysee: https://odysee.com/@ZachStar:0 Instagram: https://www.instagram.com/zachstar/ Twitter: https://twitter.com/ImZachStar Support the Channel: https://www.patreon.com/zachstar PayPal(one time donation): https://www.paypal.me/ZachStarYT Join this channel to get access to perks: https://www.youtube.com/channel/UCpCSAcbqs-sjEVfk_hMfY9w/join 2D Graphing Software: https://www.desmos.com/calculator Animations: Arkam Khan (For contact info go to https://www.arqum333.com/) Check out my Spanish channel here: https://www.youtube.com/channel/UCnkNu2xQBLASpj6cKC8vtpA ?My Setup: Camera: https://amzn.to/2RivYu5 Mic: https://amzn.to/35bKiri Tripod: https://amzn.to/2RgMTNL ?Check out my Amazon Store: https://www.amazon.com/shop/zachstar
LATEST COMMENTS